傅里叶变换公式推导,傅里叶变换性质公式张世龙06-08 15:08113次浏览

傅立叶变换(FT )傅立叶变换的目的是将时域(即时域)上的信号变换为频域)上的信号，由于对同一事物的理解角度根据区域而变化，所以在时域中有时难以处理，但在频域中比较容易处理。

傅立叶变换公式：

(w是频率，t是时间，e^-iwt是复函数) ) )。

在傅立叶变换中，一个周期函数(信号)包含多个频率成分，任意函数(信号) (f )、t )可以通过将多个周期函数(基函数)相加来合成。

要从物理上理解傅立叶变换，请使用一系列特殊函数(三角函数)作为正交基础对原始函数进行线性变换，其物理意义为原函数在各组基函数的投影。

傅立叶公式推导：我们首先从函数f(t )是周期性函数推导出来，然后推导出非周期性函数的傅立叶变换，傅里叶公式一般就是指非周期行函数的傅里叶变换（FT）。（1）对于周期为1的函数f(t)

(此处的x今后标记为t ) ) ) ) ) ) ) ) ) ) )。

欧拉公式这里的Ck是一个复数，Ck一般称为傅里叶系数，平时对频域的变换，一般改变的就是Ck。

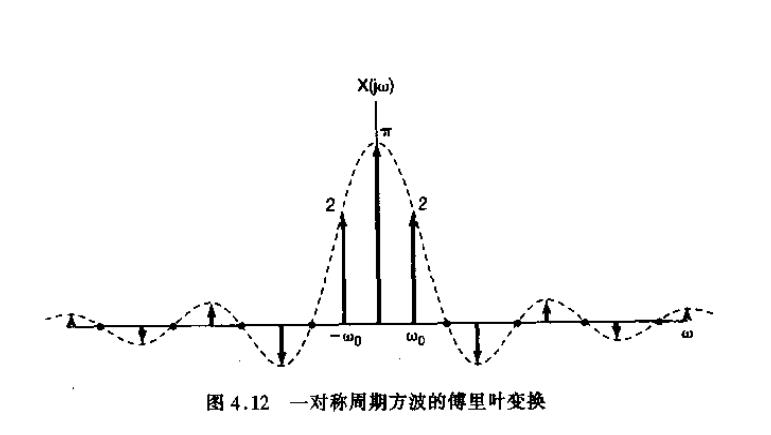
例如，该图表中频方向的图表的每个频域的值是Ck的值

接着求出Ck值

自由

对函数进行两边积分

(上述k指的是频域上的x坐标，每个k值为赫兹，且t表示时域上的时间)

为了模拟一个信号，信号不能通过有限个周期函数的相加来确定，存在大的误差，不能得到的近似，所以用无限的周期函数来近似

由此可知，傅立叶变换是时域和频域的变换关系。

（2）对于非周期函数f(t)

对于一个信号的处理，信号一般不是周期性的，所以这里会产生非周期性函数(信号)的处理。

对于非周期函数高级傅里叶公式，可假定非周期函数是具有周期函数的部分，但是该非周期函数的t范围可以非常大。 :// /

f(t )是周期为t的函数，t接近无限的周期函数

傅立叶级数[f(t ) ]是

傅立叶系数为(注：无限大的周期t，因此与0-T至(-T/2 )-) t/2 )相同)傅里叶变换当周期趋近于无穷，是傅里叶系数的一般化

这是对时域中的函数图像进行傅立叶变换后的光谱图。

重要的是： 傅里叶逆变换是对傅里叶级数的一般化

另一方面，:// /

:// /

特别是在频谱图中你看到的每一条竖线就是|CK|的值时，频谱间隔越来越近，最终为对于周期为1的函数频域上每条线的间隔为1。周期为T的函数，频域上的间隔为1/T

如果将非周期函数视为周期函数的一部分，是否会出现傅立叶变换的结果？

其实这不正确。 t无限接近时，Ck趋向零，因此傅立叶系数整体的公式没有意义。

将f(t )设为区间a、b之间的其他为0，取较大的周期t设为a-T/2bT/2，将t设为函数进行扩展(|Ck|因为是复函数所以关于x轴对称) )。

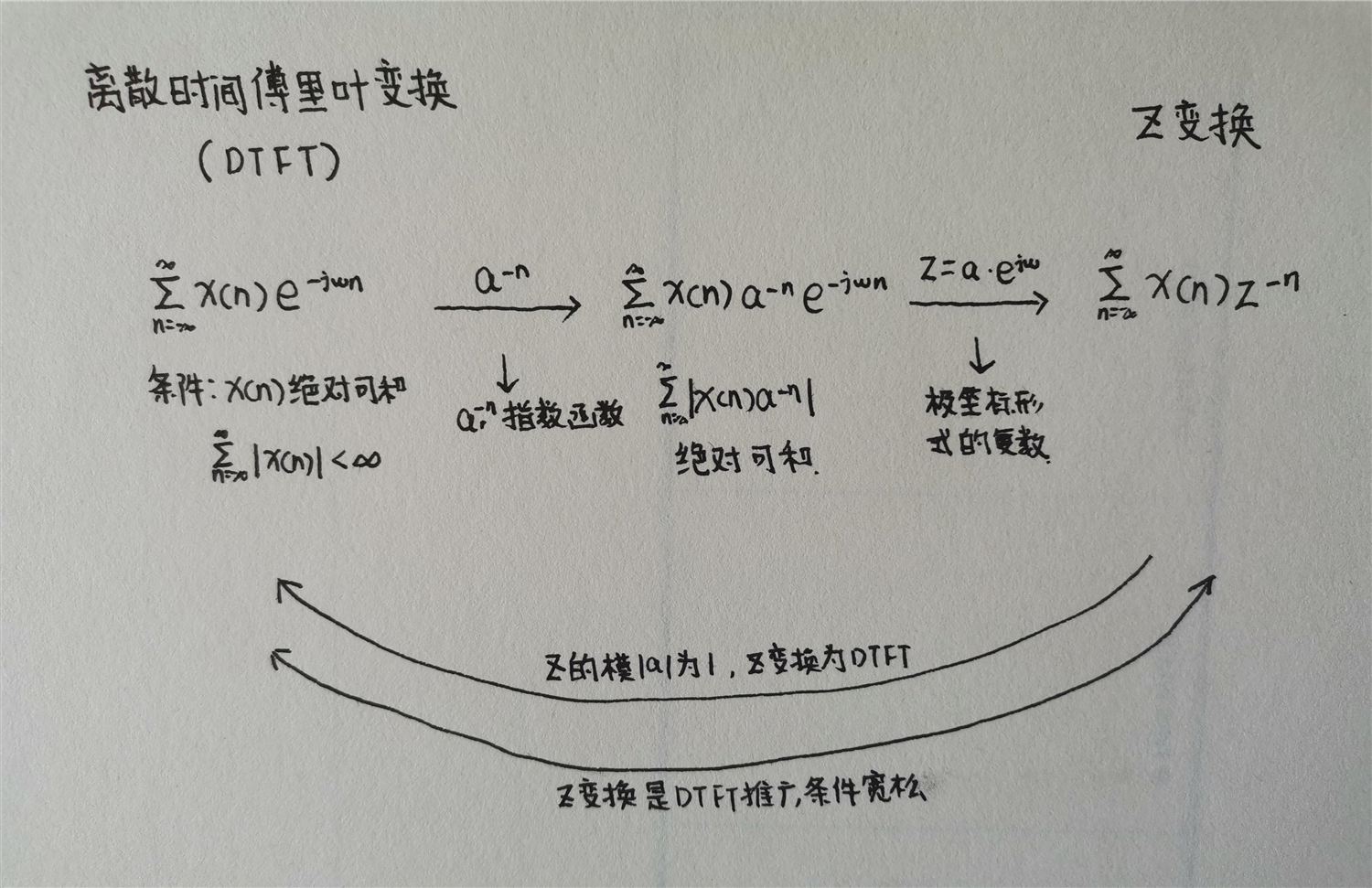
下图：

(a，b外函数为0 ) ) ) ) ) ) )。

(负指数值为1 )

此时值为固定值m

也就是说

也就是时域周期与频域有反比的关系。

即使每个频率的系数为0高级傅里叶公式，这个f(t )还有什么用？

因此，我们从另一个角度分析:3358 /

(即不需要CK1/t的部分)

(这里与上面推导f(t )的结果相同)即 T1 -1/T1 频谱会被扩展

就这样

关于f(t )，请参阅当 T1 -1/T1 频谱会被压缩，即T趋近于无穷

顺便给出傅立叶逆变换公式：

参考文章： /question/

3359 /question/

斯坦福大学课程：傅立叶变换及其应用

傅里叶变换百科,1/t的傅里叶变换